13 Mar 2024
Polya’s Problem-Solving Process

Problem-solving skills are crucial for students to navigate challenges, think critically, and find innovative solutions. In PISA, problem-solving competence is defined as “an individual’s capacity to engage in cognitive processing to understand and resolve problem situations where a method of solution is not immediately obvious” (OECD, 2014, p. 30). Returning to the classroom post-COVID, I found that students had lost their ‘grit’ for these deep-thinking tasks. They either struggled to start, gave up easily, or stopped at their first ‘answer’ without considering if it answered the problem or was the only possible solution.
To re-invigorate these skills, I investigated the impact of explicitly teaching Polya's problem-solving process in my Year Six class. This framework developed student agency and supported them to manage their feelings if they felt challenged by the work.
Here, I will share the impact of this initiative and how it empowered students to become effective and resilient problem solvers.
Understanding Polya's Problem-Solving Process
Polya's problem-solving process, developed by mathematician George Polya, provides a structured approach to problem-solving that can be applied across various domains. This four-step process consists of understanding the problem, devising a plan, trying the plan, and revisiting the solution. (Polya, 1947)
In order to focus on the skills and knowledge of the problem-solving process, I began by using tasks where the mathematical processes were obvious. This allowed me to focus on the problem-solving process explicitly.
The question shown in Figure 2 is taken from Peter Sullivan and Pat Lilburn's Open-Ended Maths Activities book. This task was used to establish a baseline assessment for each stage of the process. I planned the prompts in dot points and revealed them one by one through the PowerPoint. After launching the task and giving the students time to think, they recorded all their possible answers in their workbook.
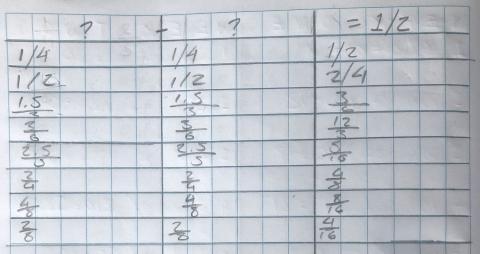
The student sample shown in Figure 3 demonstrates that the student followed a pattern and stuck to it but did not revisit their work. On line two, their response (1 half and 1 half is 2 quarters) is unreasonable.
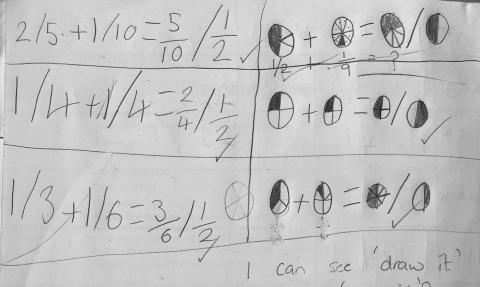
Figure 3 is a sample gathered from a small group of students. This group required support to start. They used paper folding and paper strips to model their thinking.
Over half of the class could give at least one correct answer, but only four students showed signs of checking to see if their plans addressed the problem and yielded correct answers. Understanding the problem and revisiting the solutions became the focus of my inquiry.
The following series of lessons covering operations with fractions and decimals focused on the stages of Polya’s process.
Step 1: Understanding the problem
The first step of Polya's problem-solving process emphasises the importance of ensuring you thoroughly comprehend the problem. In this step, students learn to read and analyse the problem statement, identify the key information, and clarify any uncertainties. This process encourages critical thinking (Bicer et al., 2020) as students develop the ability to break down complex problems into manageable parts. I facilitated this process by engaging students in discussions and guiding them to identify the essential components of the problem. By fostering a collaborative learning environment, students shared their perspectives and learned to refine their questions when they were unsure. Figure 6 shares an example of a prompt I use for Step 1.
Initially, students who were stuck provided the classic ‘white flag’ responses.
Student: I just don’t get it.
Teacher: What part don’t you get?
Student: All of it!
As a starting point, the students and I co-created a classroom display of helpful questions the students could use to develop their understanding.
These questions supported me to develop a deeper understanding of what students didn’t understand when they expressed uncertainty. This could range from not understanding specific terminology (often easy to explain) to where numbers came from and why their classmates interpreted the problem differently. I found engaging in this step made triaging their misunderstandings easier.
Step 2: Devising a plan
Once students had grasped the problem, the next step was to formulate a plan of action. In this step, students explored different strategies and selected the most appropriate approach. I prompted students to brainstorm possible solutions, draw diagrams, make tables, and create algorithms, all the time fostering creativity and diverse thinking.
This step had been a strength during the baseline assessment data, and a wide range of strategies were explored. Polya’s strategies were displayed in the classroom as the mathematician’s strategy tool kit, so students were comfortable acknowledging the many ways to solve the problem.
Students developed critical thinking and decision-making skills by keeping this step in problem-solving. They become adept at evaluating multiple approaches and selecting the most effective strategy to solve a problem, thus promoting the development of mathematical reasoning abilities (Barnes, 2021). Figure 7 shows a slide used in Step 2.
Step 3: Try
The students implemented their selected strategy, performed calculations, made models, drew diagrams, created tables, and found patterns. This stage encouraged students to persevere and take ownership of their problem-solving process.
At Cowes Primary School, we have developed whole-school expectations around providing opportunities for hands-on learning, allowing students to engage in practical activities that support the development of ideas, expecting students to represent their work visually (pictures, materials and manipulatives), using language and numbers/symbols. This approach enhances students' problem-solving skills and fosters a sense of autonomy and confidence in their capabilities and ability to talk about their work (Roche et al., 2023). Figure 9 shows the slide used for Step 3.
Step 4. Re-visiting the solution
The last step in Polya's problem-solving process is re-visit. After finding a solution, students critically analyse and evaluate their approach after finding a solution. They consider the effectiveness of their chosen strategy, identify strengths and weaknesses, and reflect on how they could improve their problem-solving techniques. This step was missing from most students’ work during the baseline assessment.
As a class, we added to the display questions to facilitate better reflective practice and developed a more critical approach to looking at our work. This process encouraged students to refine their answers, not go too far down the wrong path, fostered resilience, embrace challenge and normalise uncertainty (Buckley & Sullivan, 2023).



Impact and benefits
Figure 9 shows four tasks, including the initial baseline assessment. The blue series shows the percentage of students who arrived at least one correct solution. The green series shows evidence that students were revisiting their initial solutions using other strategies to check they were correct or checking in with other groups and adjusting. There was a steady increase in both skills over the course of these four tasks.
By explicitly teaching Polya's problem-solving process, the students cultivated valuable skills that extend beyond maths problems. Some of the key benefits observed were:
Mathematical Reasoning: Polya's process promotes the development of mathematical reasoning skills. Students analysed problems, explored different strategies, and apply logical thinking to arrive at solutions. These skills can enhance their overall mathematical proficiency.
Self-efficacy: Through problem-solving, students gained confidence in their ability to tackle problems. They become more self-reliant, taking ownership of their learning, and seeking solutions proactively.
Collaboration and Communication: The process encouraged collaboration and communication among students. They discussed problems, shared ideas, and considered multiple perspectives, students developed effective teamwork and interpersonal skills.
Metacognition: The reflective aspect of Polya's process fostered metacognitive skills, enabling students to monitor and regulate their thinking processes. They learned to identify their strengths and weaknesses, supporting continuous improvement and growth.
Conclusion
Overall using the 4 steps was a really effective and an explicit way to focus on developing the problem-solving skills of my Year 6 students.
This article was originally published for the Mathematical Association of Victoria's Prime Number.
References
- Barnes, A. (2021). Enjoyment in learning mathematics: Its role as a potential barrier to children’s perseverance in mathematical reasoning. Educational Studies in Mathematics, 106(1), 45–63.
- Bicer, Ali, Yujin Lee, Celal Perihan, Mary M. Capraro, and Robert M. Capraro. ‘Considering Mathematical Creative Self-Efficacy with Problem Posing as a Measure of Mathematical Creativity’. Educational Studies in Mathematics 105, no. 3 (November 2020): 457–85.
- Buckley, S., & Sullivan, P. (2023). Reframing anxiety and uncertainty in the mathematics classroom. Mathematics Education Research Journal, 35(S1), 157–170.
- OECD (Ed.). (2014). Creative problem solving: Students’ skills in tackling real-life problems. OECD.
- Pólya, G. (1988). How to solve it: A new aspect of mathematical method (2nd ed). Princeton university press.
- Roche, A., Gervasoni, A., & Kalogeropoulos, P. (2023). Factors that promote interest and engagement in learning mathematics for low-achieving primary students across three learning settings. Mathematics Education Research Journal, 35(3), 525–556.





